如果你想系统学习卷积神经网络(CNN),我强烈推荐先访问这篇由 Georgia Tech 与 Oregon State 联合出品的可视化教程:CNN Explainer。这是一个专业、严谨、交互性强的教学项目
虽然这篇教程提供了非常专业的可视化教程,图示清晰、结构严谨,但对初学者而言仍可能有些“云里雾里”:术语密集、上下文要求高,稍不留神就会被各种名词绕晕
因此,我写下了这篇面向零基础读者的 CNN 比喻笔记,用一个简单而持续统一的类比设定,把整套知识体系“讲成一个故事”,像看侦探小说一样,逐步理解 CNN 的核心逻辑和每个模块的作用
在这篇笔记中,我们会将 CNN 想象成一套“城市侦查系统”,通过无人巡逻机、特征探测器、报警器、信息压缩员、指挥中心、评分官等角色,把看似抽象的算法过程,具象化为一次图像中的“破案行动”
为了展开这个比喻,我们先从最基础的认知出发:卷积神经网络(CNN)是一种特别擅长处理图像的深度学习模型
我们不妨设定这样一个背景:把一张图像想象成一座庞大的城市,而我们的任务,是找出城市中是否存在嫌疑人活动的区域(从图像中找出我们所需要的目标)。由于城市范围太大,不可能一眼看全,所以无人机必须一块一块地带着探测器在城市上空巡逻,每次只观察一个小片区,判断是否有可疑线索
城市侦查体系的角色设定(对应 CNN 各模块)
我们先把这套“ 城市侦查体系 ”中每个角色的职责清楚列出来。每一个角色,都对应着 CNN 结构中的一个关键模块:
| 现实比喻中的角色 | CNN 中的概念 | 职责说明 |
|---|
| 城市 | 图像(imgae) | 整张待分析的图像,城市的每一个街区即一个像素 |
| 无人巡逻机 | 滑动窗口(Sliding Window) | 搭载探测器,固定路径巡视城市每个区域 |
| 特征探测器 | 卷积核(Kernel) | 权重矩阵型,装在无人机上,识别特定线索,如边缘、纹理、角点等 |
| 侦查打分记录 | 神经元(Neuron) | 每次巡逻无人机在某个区域留下的判断打分(可疑分数) |
| 多队侦查指令 | 卷积层(Conv Layer) | 发起本轮侦查,多个无人机携带探测器(卷积核)全面巡视 |
| 探测器警觉线 | 偏置项(Bias) | 给每个探测器加上个性偏好,决定其整体判断倾向 |
| 报警器 | 激活函数(Activation Function) | 判断线索是否强烈,是否触发响应 |
| 信息压缩员 | 池化层(Pooling) | 提取区域内最强线索,丢弃无效数据 |
| 指挥中心 | 全连接层(FC Layer) | 整合全图信息,输出分类/判断结果 |
| 评分官 | 损失函数(Loss) | 判断这次判断对不对,错了多少 |
| 复盘小组 | 反向传播(Backprop) | 回头找出错的步骤,标记修改方向 |
| 教官 | 优化器+梯度下降 | 调整配置,提升未来判断能力 |
有了这张“角色对照表”,你就可以在后面的每一节中代入这些现实角色去理解 CNN 的每一步是怎么运行的,避免被生硬术语绕晕
数据预处理(Data Preprocessing)
首先将照片比喻为一座“城市”,我们需要知道,图像作为城市是由 红、绿、蓝三个滤镜 构成的三通道画面(可以看作是三个矩阵叠成的一座“数字城市”,它的数学结构是一个大小为 3×H×W 的张量(tensor):三个通道 × 高度 × 宽度 )。
每个街区(像素)在这三个滤镜下的亮度各不相同,比如某个街区的原始数值是:
- 红通道:23(偏暗)
- 绿通道:145(偏亮)
- 蓝通道:56(中等)
这说明同一个街区,在不同颜色滤镜(通道、维度)下的“可见度”是完全不同的
但问题在于:每个通道的数值分布并不一致,有的通道整体偏亮,有的偏暗。如果我们不先做统一处理,系统就可能“误判”某些街区的重要性——以为那里很突出,其实只是因为某个颜色通道整体偏高
你可以把这理解为汇率问题:就像同样是“100”,出现在欧元或津巴布韦币上,其实际购买力却大相径庭。要想准确比较不同通道的“亮度权重”,我们就得把它们统一成一个共同的标准尺度——就像先都换算成“美元”,才能真正评估各自的价值(即该像素在模型眼中的重要性)
因此,我们需要先进行标准化操作:
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))
])
在代码中,这一步由以下操作完成:
ToTensor():将PIL图像或NumPy数组转换为PyTorch张量,并自动将像素值[0 - 255]归一化到 [0, 1]Normalize():均值-方差标准化,对图像进行标准化,公式为:(x - mean) / std,使数据符合零均值和单位方差(mean = 0,std = 1),统一各通道亮度到标准范围(如 -1 到 1),消除不同滤镜间的“光照偏差”,确保系统能公平分析每个颜色通道的线索
这样一来,图像就被“打磨”为一份清晰、整洁、统一格式的“城市”,正式准备好交给城市侦察系统分析,不会因某一通道偏亮或偏暗而产生误判
💡 是否所有图像都需要这样处理?
并非绝对。RGB三通道 + 统一归一化是一种最常见的入门设置,特别适用于彩色图像分类任务(如 CIFAR、ImageNet)。但在灰度图(如 MNIST)、医疗图像、多光谱图像等任务中,预处理方式可能不同,甚至可能完全跳过标准化步骤,改为更适合该任务的数据增强或通道转换。因此,这套方法适用于多数“标准图像识别入门场景”,但具体还需视任务而定
卷积核(Convolutional Kernel)
在我们的城市侦查系统里,负责在图像这座“城市”中挨家挨户排查可疑活动的,是一批配备了特征探测器的无人巡逻机(对应 CNN 中的滑动窗口 Sliding Window)。而这些无人机上搭载的最关键设备,就是特征探测器,也叫卷积核或滤波器(Convolutional Kernel)
这个特征探测器是什么
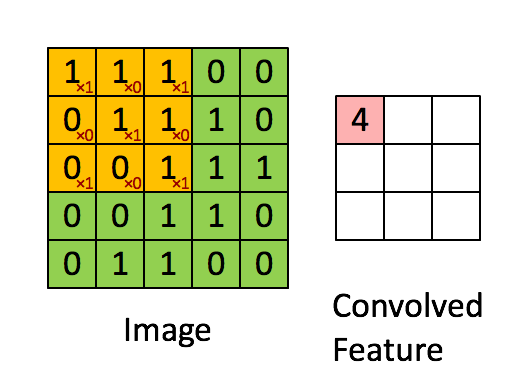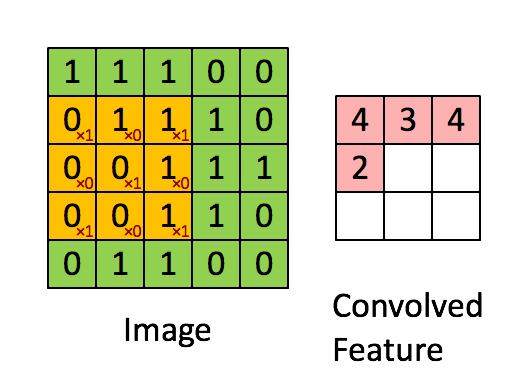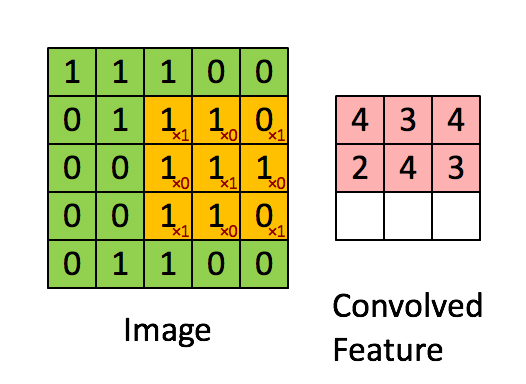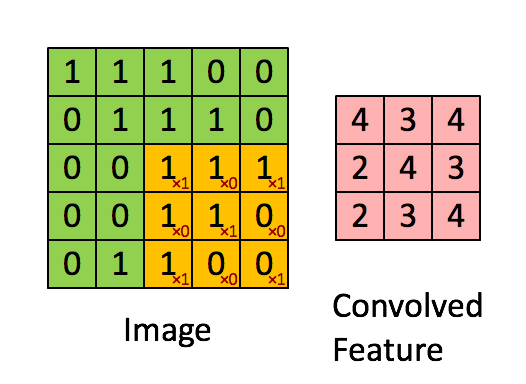
每个特征探测器就像一块 3×3 (也可以是5×5之类的其他数字,这里拿 3×3 举例)的微型扫描器(权重矩阵),它一次只能关注城市中的一个小区域——就是3行3列的街区,也就是图像中的 9 个像素格子。这就像无人机通过一个一次仅能看到 9 个街区的小范围来观察城市局部
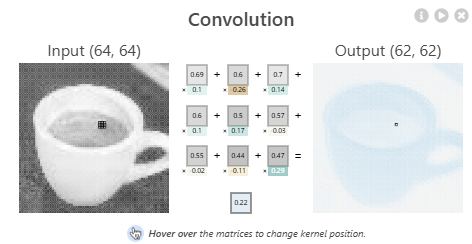
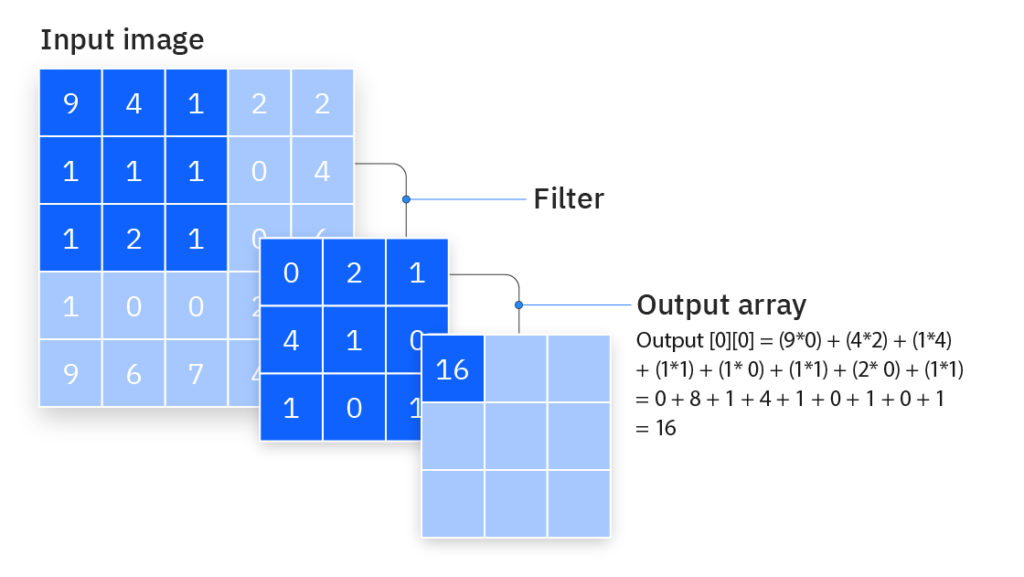
特征探测器的任务是:对这 9 个像素应用一套「观察模板」,用模板里的9个数值(下图中的0.69...0.47)分别去乘上对应9个像素(下图中的 0.1...0.29)的“热度值”(像素亮度,数值越大表示越亮(这里也被称为”一次激活/激励“),然后全部加起来,算出一个代表这个区域“可疑程度”的分数(下图中的 0.22), 也就是神经元(Neuron)
 CNN explainer : 中间灰色部分为像素,其下方的彩色部分为“模板”
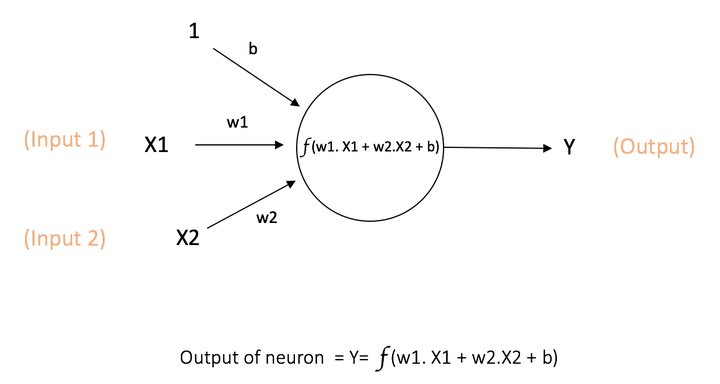
CNN explainer : 中间灰色部分为像素,其下方的彩色部分为“模板” 神经元示意图,与上图原理一样,此网络接受 X1 和 X2 的数值输入,权重分别为 w1 和 w2。还配有权重 b(称为偏置(bias )的输入 1
神经元示意图,与上图原理一样,此网络接受 X1 和 X2 的数值输入,权重分别为 w1 和 w2。还配有权重 b(称为偏置(bias )的输入 1
每个神经元是一个多输入单输出的线性叠加单元这组“观察模板”的 3×3 每一个数字,其实就叫做:
权重(Weight) —— 代表这个探测器对每个位置的“关注程度”与“判断倾向”
比如:
- 数值大 → 表示特别敏感,影响评分更多
- 正值 → 表示“看到亮的就加分”
- 负值 → 表示“看到亮的要减分”
- 是 0 → 表示“这个点我不在意”
举个例子,这是一种经典的边缘探测器 「观察模板」 :
[-1, -1, -1]
[ 0, 0, 0]
[ 1, 1, 1]
它特别擅长识别“上暗下亮”的局部结构——比如:
- 如果图像上半部分较暗、下半部分较亮,它就输出一个很高的分值,说明可能是一个“水平边界”,比如人脸下巴或物体的边缘
- 如果区域整体亮度差不多,输出就很低,说明这个片区平平无奇
不过这只是其中一种探测器的类型,实际上,不同的卷积核会逐渐形成自己的“探测专长”:
- 有的专门识别斜线
- 有的关注颜色过渡
- 有的擅长发现圆形结构
- 甚至有的在更深层网络中能识别人脸、轮廓、窗户等复杂结构
那问题来了:这些“探测模板”是谁设计的呢?
答案是——谁都没有直接设计
这些卷积核的数字并不是人提前设定的,也不是告诉它“你来识别边缘,你来识别圆形”之类的安排。它们一开始是随机的,就像一批新警察刚入职,每个人的直觉五花八门,没人知道自己到底擅长啥,有些人随机地关注马路,有些人盯着人行道,有些人甚至看云彩
但在后期的系统经过一次次“实战巡逻”(前向传播)和“案件复盘”(反向传播)之后,评分官指出哪里判断错了,教官(优化器)就会根据错误反馈来调整这些模板里的数字(权重)
于是,这些探测器就像警察一样,在反复训练(也就是模型训练)中逐渐形成了各自的“特长”:有的学会识别边缘、有的擅长找圆形、有的能发现面孔或车轮。没有人告诉它们怎么做,是它们自己学出来的
注意:我们需要特别理解卷积中两个重要且严谨的特性:
- 局部感知机制:每个卷积核在扫描图像时只关注一小块区域(如3×3、5×5),不会直接观察整张图。这就像巡逻无人机只能看到一小片街区,做出局部判断。这种机制让模型更擅长捕捉局部特征(如边缘、纹理、角点等)
- 权值共享:同一个卷积核在滑动窗口过程中,使用的是同一组权重值(也就是一套固定的“侦察模板”),无论它在哪个位置扫描,都会用同样的方式去打分。这大大减少了需要学习的参数数量,让模型在记忆能力强的同时也不容易过拟合。如果没有权值共享,假设输入图像大小为 1280×720,我们希望提取 1000 个特征,那意味着每个像素点都要和每个特征神经元连接: 1280×720×1000=92,160,000 个参数,而权值共享:只需要设计 1000 个 5×5 的“特征探测器”(卷积核),共享参数滑动侦查即可: 5×5×1000=25,000 个参数
滑动窗口(Sliding Window)
回到故事中,当无人机携带者特征探测器每次查看一块 3x3 区域后,会向右、向下逐步滑动,继续下一块区域的扫描。这个“一块块移动”的策略叫滑动窗口。
- 如果滑动步长(stride)为 1,就是一格一格扫,特别细致;
- 如果 stride 为 2,就隔一格扫,更快但可能略过细节
我们需要特别说明的是:
- 这里的“3×3”窗口本身已经包含了周围多个街区的范围,也就是说,它一次观察的区域就横跨了邻近的格子
- 即便步长 stride 设置为 2,每次滑动两个格子,也不意味着完全跳过了中间区域。因为每个 3×3 的侦察窗口本身就覆盖了多个街区,它在不同位置之间是有重叠的,能捕捉到大部分图像区域的信息
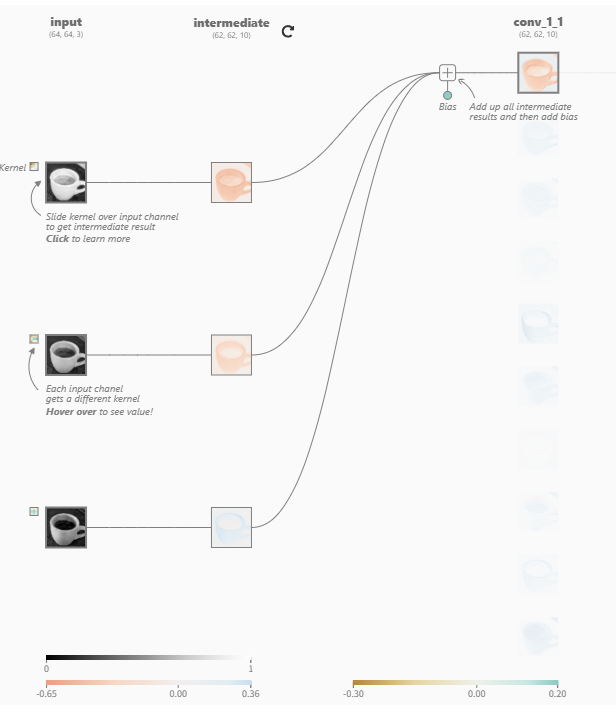
当滑动窗口从图像的左上角出发,一块块地完成所有区域的扫描并打分之后,整个图像就被这一套特征探测器“巡视完毕”了,此时会得到一张“打分图”(下图中的intermediate),不过这还不是最终结果。在输出这张“打分图”之前,系统还会为每组探测器的结果加上一个 “微调项” —— 我们称之为 偏置(Bias)
以下图的 RGB 图像为例:红、绿、蓝三个通道各自配备了自己的探测器(卷积核),分别扫描全图后得到三张中间“打分图”。这些打分会被叠加合成,然后再加上一个偏置值,作为最终输出(conv_1_1)的特征图(Feature Map)
这个偏置值可以理解为一个特征探测器的“个性”:
- 偏置为正:偏紧张,总想报案,多给点分(容易被激活)
- 偏置为负:偏佛系,就算看到轻微线索也觉得无所谓,整体压低打分(较为冷静,必须看到更强的线索才触发)
- 非常严谨地说,偏置(Bias)的核心目的:为了提升模型的表达能力,让它即使在没有任何输入特征激活的情况下也能输出有效结果
每一张输出特征图都对应一个独立偏置,在训练过程中会随着卷积核一起被优化
需要注意:
- 特征图这个词只代表:卷积操作后生成的一张二维矩阵,表示某一类特征在图像中的空间分布,但是在实际计算特征图时,这个过程通常包括了加偏置的步骤:特征图 = 卷积核 * 输入 + 偏置(特征图的“定义”本身不包含“偏置”的概念,但在计算特征图的数值时,通常会加上偏置项)
在卷积神经网络中:
- 单通道输入:一个卷积核 + 一个偏置,产生一个特征图;
- 多通道输入:多个对应通道的卷积核协同工作,卷积结果相加 + 一个偏置,合并成一个特征图
举个例子:
- 输入是
3通道(如 RGB 图像); - 我们要生成
32 张特征图; - 那么卷积核个数是:32组(32个单个通道上的二维权重矩阵) × 每组3个卷积核(每通道1个) = 96;
- 对应的参数量是
96个 kernel + 32个 bias。
不过,一张特征图远远不够。不同的探测器擅长识别不同类型的线索,要更全面地理解图像,就需要多个特征探测器协同出动——这就是卷积层的工作范畴
卷积层(Convolutional Layer)
在城市侦查系统中,我们前面已经介绍了单个特征探测器(卷积核)如何通过滑动窗口在城市中巡视,并生成一张初步的“特征图”——这张图可能仍带着“新警察”式的稚嫩判断,仅能反映某一类可疑线索的分布情况
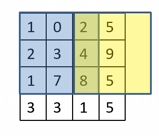
不过在执行这种扫描任务时,我们还会遇到一个实际问题:城市边缘的街区常常被漏扫。为什么?因为特征探测器的“巡视窗”通常是 3×3,如果你从城市左上角开始滑动,当滑到最右边或最下边时,窗框很可能已经“探不到”最边缘的街区,只能看到一部分
这就好比扫地机器人扫地时,总是卡在墙角扫不干净。为了让边角区域也能被完全侦查,我们在图像四周加上一圈“虚拟街区”作为缓冲,这种操作叫做 Padding(填充)
这些虚拟街区可以是全黑的(0值),它们不会提供额外信息,但能让真正的边缘街区也进入卷积窗口的视野中,不被遗漏
因此 Padding 不是为了改变内容,而是为了让边缘也拥有平等被巡逻的机会,避免模型“只重视中间,忽略边角”
 右侧的黄色区域会被填充0
右侧的黄色区域会被填充0有了这个准备之后,我们就可以展开真正的大规模侦查任务了
卷积层作为整支警队的行动指挥部,发起了第一轮侦查命令:一次性派出多个侦察无人机小队,每个小队配备一套不同功能的探测器,分别擅长发现不同类型的线索(如边缘、角落、图案等),共同对整座城市进行全面排查
卷积层的职责是
- 派出一批无人机(滑动窗口)
- 每架无人机配一个不同的特征检测器(卷积核)
- 这些特征检测器会滑动扫描图像,一块块“打分”
- 每一组“打分结果”就会生成一张特征图(feature map)
比如:
- 边缘探测器 → 边缘强度图
- 圆形探测器 → 圆形分布图
卷积层结构总结
| 项目 | 说明 |
|---|
| 输入 | 原始图像 或 上一层输出的特征图堆叠 |
| 操作 | 多个卷积核进行滑动卷积运算 |
| 输出 | 多张特征图(每个卷积核生成一张) |
这些特征图会被统一堆叠,作为下一层的输入,就像收集了多种情报版本,等待后续更深入的分析

激活函数(Activation Function)
在城市侦查系统中,特征探测器(卷积核)巡视每一片区域后,会输出一个“可疑程度评分”。但系统不会立刻相信所有评分,而是需要一个判断机制来决定:
“这个评分够高吗?是否值得进一步处理?”
这个机制,就是激活函数,它就像系统中的“警报器”或“电闸”:
- 分数高 → 触发警报,信号放行
- 分数低 → 静音处理,信号被压制
激活函数是在每次卷积计算之后,立刻执行的
- 卷积核滑动覆盖一个小区域(如3×3),做一次点积计算
- 得出一个数值(比如 2.5 或 -0.3)
- 这个数值立刻送入激活函数做判断
- 激活后的结果才被写入特征图中对应的位置
所以你可以理解为:卷一次 → 激活一次 → 写入一次,这个过程反复进行,生成整张特征图
而不是:先整张图卷一遍再统一激活,或者先卷完所有图再触发警报。每一个“评分点”都要逐一判断是否值得保留
 ReLU: 𝑓(x) = max(0, x) -0.32被静音处理
ReLU: 𝑓(x) = max(0, x) -0.32被静音处理为什么需要激活函数?
现实世界的判断行为是非线性的:
- 看见一点灰毛 ≠ 是猫
- 看见耳朵 + 胡子 + 躯干 → 才突然意识是猫
没有激活函数,整个 CNN 就只能做“线性计算”,哪怕叠 100 层都只是一个加权器。无法做“有条件地反应”的判断。
所以:激活函数赋予网络“非线性能力”,让它能做出“够不够强 → 是否触发”这样的真实决策行为
常见的激活函数(及比喻)
| 激活函数 | 数学表达 | 比喻 | 特点 |
|---|
ReLU
Rectified Linear Unit | 𝑓(x) = max(0, x) | 单向警报器:分数只要高于 0 就响铃 | 简单高效,是 CNN 默认首选 |
| Sigmoid | 𝑓(x) = 1 / (1 + e^(-x)) | 门槛式警报器:越高越响,0 附近不响 | 输出范围 0~1,常用于二分类 |
| Tanh | 𝑓(x) = (e^x - e^(-x)) / (e^x + e^(-x)) | 双向警报器:强烈正向/负向都能触发 | 输出范围 -1~1,适用于对称任务 |
在这里对比一下偏置和激活函数的区别以免混淆:
| 对比项 | 偏置(Bias) | 激活函数(Activation Function) |
|---|
| 位置 | 卷积/加权求和后,激活函数前 | 在偏置之后,用于变换输出 |
| 作用 | 调节单个区域分数(神经元)整体“输出水平”,可以让神经元在没有输入信号时也“激活” | 给网络加入非线性能力,模拟复杂决策边界 |
| 可学习性 | ✅ 是可训练参数,训练中会被优化 | ❌ 是固定公式(如 ReLU、Sigmoid) |
| 比喻类比 | “心理基准线”“个人习惯加分项”“个人情绪” | “是否触发警报的门槛机制”“规章制度” |
| 影响范围 | 每个神经元单独一个数值(可调) | 所有神经元用同一个函数(不可调) |
池化层(Pooling Layer)
卷积层和激活函数已经完成了“侦查”和“判断”的工作,接下来进入 CNN 的信息处理环节中的第三步 —— 池化层。它的作用是:在保留最关键线索的同时,大幅减少图像尺寸,降低计算成本
我们可以把池化层比喻成一个 信息压缩员 ,每扫完一个片区后,他会对多个相邻街区的情报进行浓缩,只保留最重要的部分,其余的琐碎细节一律不汇报
池化机制:如何“压缩信息”?
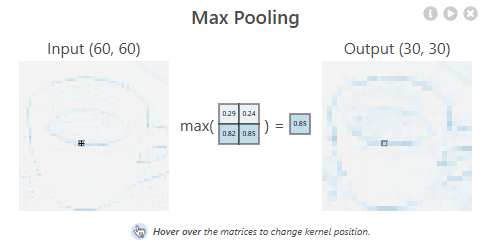
池化通常以一个 2×2 的滑动窗口为单位,在图像上“降采样”
- 最大池化(Max Pooling):每个小区域中只保留最大值,其他数值全部丢弃
- 这就好比在一个街区里选出最显眼的事件(比如一栋失火的建筑),其他的吵架、乱停车之类的就不提了
这种方式能让 CNN 在图像尺寸减半的同时,保住最显著的特征
 Max Pooling 保住最显著的特征
Max Pooling 保住最显著的特征夏洛克·福尔摩斯的“阁楼理论”
池化层很符合夏洛克那句经典台词:
“大脑就像一个阁楼,聪明人只存放最有用的信息。”
池化发生在哪一步?
池化是在 卷积 + 激活函数之后 进行的。
完整顺序是:图像 → 卷积 → 激活函数判断是否报警 → 池化层做摘要 → 下一层输入
所以你可以理解为:“警报”响了之后,池化层判断这些响过的警报中,哪些才是真的值得记录在案
常见的池化方式
| 池化方式 | 说明 | 比喻 |
|---|
| Max Pooling | 保留每个小区域中的最大值 | 报告最严重的事件 |
| Average Pooling | 取平均值,保留整体趋势 | 报告区域的整体态势 |
| Global Average Pooling | 每张特征图只保留一个平均值 | 把整个城市的线索浓缩成一个大结论 |
现代 CNN 中,Max Pooling 使用最广。部分新架构甚至用 Global Average Pooling 代替全连接层
全连接层(Fully Connected Layer)
经过多轮“侦察”与“线索筛选”(即卷积层和池化层),整座城市的关键信息已经被提取成了一张张“特征图”。但此时的信息依然是局部碎片:这块区域有边缘,那块区域有圆形……还没有人把它们汇总为最终判断
这时,全连接层就像是城市指挥中心召开的一场终极决策会议:各路线索被逐条整合交付给决策者,系统要基于全图信息做出最后判断,所谓“全连接”,就是决策系统中的每一个判断单元(也叫输出节点或神经元)都会接收到上一层的所有线索数据,不再局限于某一片街区。这种设计保证了每个判断都是基于全局特征,而不是片面结论
注意:
这里再次提到了神经元,神经元在在卷积层滑动窗口汇总的 3X3 可疑程度分数被我们比喻为巡逻无人机在某片3X3街区留下的判断结果,然而到了全连接层,神经元的角色变了:它们不再关注局部,而是每一个都接收了整张图像的所有线索,在后期是指挥中心中的一位“决策者”,CNN 中的 “神经元” 在不同阶段,承担了不同粒度的角色,语义和维度会随着层级上升而变化,这是初学者最容易产生困惑的点之一
决策流程是怎么进行的?
整个决策过程大致分为以下几步:
- 展平(Flatten):系统会先将卷积/池化层输出的多维特征图(比如 13×13×10)拉直为一条长长的一维向量(比如 1690),就像把一张地图拆成线索清单,每条线索都编号排列,准备提交给判断节点
- 评分决策:此时每个判断节点(神经元)都会接收到整份线索清单——也就是这 1690 个数。它会对每条线索赋予不同的重要性(称为权重 weight),然后再加上它自己的“判断倾向”(即偏置 bias),最终输出一个总分 logit = w₁·x₁ + w₂·x₂ + … + w₁₆₉₀·x₁₆₉₀ + b
- 最终打分与分类决策:每个判断单元都会输出一个 logit(未归一化得分),组成一个打分列表:
嫌疑人 espresso → 5.2
嫌疑人 B → 1.8
其他 → 0.3
但这些原始分数还不能直接拿来比较——因为它们既可能为正也可能为负,范围也不同。我们需要统一标准,让它们变成类似“概率”的形式,于是,下一步就是使用 Softmax 函数(确保 CNN 输出之和为 1。因此,softmax可用于将模型输出缩放为概率)将 logits 转换为概率
嫌疑人 espresso → 0.88
嫌疑人 B → 0.08
其他 → 0.04
这意味着模型“有 88% 的把握认为图中是 espresso”,因此最终预测就是它
简单计算例子:三分类全连接层
假设:
- 上一层的输出被展平成一个向量:
输入向量 x = [0.2, 0.6, 0.4] - 我们的任务是从中判断这张图像属于哪一类:
A类、B类、C类 - 全连接层有 3 个输出节点(每个节点对应一个类别)
每个节点都有自己的权重 + 偏置
第一步:加权求和(计算 logits)
我们用公式: z=w1x1+w2x2+w3x3 +b
分别设置三个判断单元(即 3 个输出神经元)的权重和偏置:
| 类别 | 权重 w | 偏置 b | 计算公式 | 结果 z (logit) |
|---|
| A | [0.1, 0.3, 0.5] | 0.2 | 0.1×0.2 + 0.3×0.6 + 0.5×0.4 + 0.2 = 0.64 | 0.64 |
| B | [0.4, 0.1, 0.2] | -0.1 | 0.4×0.2 + 0.1×0.6 + 0.2×0.4 - 0.1 = 0.17 | 0.17 |
| C | [0.2, 0.6, 0.1] | 0.0 | 0.2×0.2 + 0.6×0.6 + 0.1×0.4 + 0.0 = 0.52 | 0.52 |
第二步:Softmax 归一化(得到概率)
我们将 3 个 logit:[0.64, 0.17, 0.52] 代入 Softmax:
计算自然指数函数(e 是自然对数的底数,约为 2.71828):
- e0.64 ≈ 1.896
- e0.17 ≈ 1.186
- e0.52 ≈ 1.682
- 总和 = 1.896 + 1.186 + 1.682 = 4.764
概率分布:
- A 类:1.896 / 4.764 ≈ 0.398
- B 类:1.186 / 4.764 ≈ 0.249
- C 类:1.682 / 4.764 ≈ 0.353
✅ 最终判断
虽然 A 的打分最高,但 Softmax 之后的概率也很接近:
- A 类:39.8%
- C 类:35.3%
- B 类:24.9%
系统可能最终选 A 类作为预测结果(最高概率)
全连接层在整体流程中的位置
整个 CNN 的数据流如下:
卷积层 → 激活函数 → 池化层(反复堆叠) → 拉平成向量 → 全连接层 → 分类输出
提示:
虽然现代 CNN 架构中有时使用“全局平均池化”替代全连接层,以减少参数数量,但理解全连接层的“信息整合 → 分类判断”机制,对于初学者掌握神经网络的整体逻辑仍然非常重要
损失函数(Loss Function)
当卷积层提取了特征、池化层浓缩了线索、全连接层做出判断后,CNN 模型终于完成了它的第一次“侦破任务”。但问题来了: 模型自己说“这是嫌疑人”,那它到底说得对不对?谁来打分?
这就轮到损失函数登场了,它的角色就像是城市指挥中心的评分官,负责给模型的每一次判断打分,告诉它:
- 你说得太离谱了,扣你 90 分
- 你猜得还行,稍有偏差,扣你 15 分
- 你答对了,给你满分!
为什么评分官“知道答案”?
你可能会疑惑:“我们不是在找嫌疑人吗?那评分官怎么好像早就知道答案似的?”
这其实是监督式学习的基本设定:在模型训练阶段,我们每张图像都已经打好了标签(比如“这是数字7”、“这是猫”)。损失函数就是根据这些我们手里已有的标准答案,来核对模型的判断,然后给出一个评分(loss 值)
所以你可以理解为——模型是个新手侦探,而评分官是背着答案在旁边看他表现的考官
🎬 电影《源代码》里的评分机制
如果你看过电影《源代码(Source Code)》,你会发现主角的经历和训练神经网络惊人地相似:
- 主角一次次回到列车爆炸发生前
- 每次都猜一个人是恐怖分子
- 系统知道谁才是凶手
- 每次猜错,系统就把他打回原点:“不对,重来!“
- 他从失败中学习,最终锁定目标
这就和损失函数的角色一样:每次模型猜完,损失函数就像源代码系统那样说一句:“你错了多少”,然后让模型开始下一轮回溯和改进
最常用的评分方法:交叉熵(Cross-Entropy Loss)
在分类任务中,最常见的损失函数就是交叉熵。它的思路是:
- 模型输出每个类别的概率;
- 如果它把正确类别的概率压得很高(比如接近 1) → 得分很低(好);
- 如果它把正确答案的概率压得很低 → 得分很高(糟糕)!
这就像说:
“你不但猜错了,而且还非常自信地猜错了” → 重罚!
损失函数在流程中的位置?
你可以把 CNN 的整个推理过程看作一次办案演练,损失函数就是最后的评分步骤:
图像输入 → 侦查线索提取(卷积/池化) → 全局判断(全连接) → 输出 → ⚠️ 损失函数打分
打完分,才会进入下一步:反向传播去查错(就像源代码主角回忆哪里判断失误了)
| 任务类型 | 常用损失函数 | 预测输出 | 推荐激活函数 | 典型应用 |
|---|
| 二分类 | Binary Cross Entropy | 单个概率(0~1) | Sigmoid | 用于二元输出,如真假、是非问题
判断是否为猫 |
| 多分类(互斥) | Cross Entropy | 多类概率和为1 | Softmax | 识别数字0~9 |
| 回归任务 | Mean Squared Error | 连续数值 | 通常无(或 ReLU) | 预测房价、温度 |
| 多标签分类 | BCEWithLogitsLoss | 每类独立概率(0~1) | 无(内置 Sigmoid) | 图中同时含猫狗 |
| 图像分割(二类) | Dice Loss / BCE | 每像素一个概率 | Sigmoid | 前景/背景分割 |
| 图像分割(多类) | Cross Entropy / Dice | 每像素一个类别 | Softmax | 语义分割(如道路/人/车) |
| 目标检测 | IoU Loss / GIoU / Focal Loss | 边界框 + 类别 | Sigmoid(多数框架用) | 检测人脸、车辆、物体 |
反向传播(Backpropagation)
CNN 已经完成了一次完整的“办案流程”:看图 → 找线索 → 判断嫌疑人 → 被评分官打了分(前向传播)
但如果每次都只是告诉模型“你错了”,却不告诉它错在哪儿、怎么改,那它永远也学不会
这时候就该叫出城市侦查系统中的复盘小组——反向传播机制(Backpropagation)!
反向传播在干什么?
它负责把损失函数打出的“错误分数”,反向传递回模型内部,从输出层一直传回最前面的卷积核,告诉每一层:
- “你刚才的判断对最终错误的影响有多大”
- “你该怎么调整你自己的行为”
你可以理解为模型在一次失败的推理之后,进行了一次深度复盘审查(模型通过前向传播完成了推理过程,我们得到了评分(损失函数)。接下来,我们就通过反向传播,把这个“错误分数”逐层传回去,对每一层进行复盘和修正)
还记得《源代码》吗?
主角在被系统判定“判断错误”之后,并不是直接放弃任务,而是:
- 回忆自己刚才“看漏了什么”
- 推演哪些行为可能导致错误结论
- 然后下一轮改正方向,越来越接近目标
这正是反向传播在做的事:根据评分误差,从后往前一层一层查清楚“到底是哪一步出的问题”,并计算出该层需要调整多少参数
它到底是怎么“查错”的?
每一层的神经元都记录了:
- 自己接收了什么输入
- 输出了什么结果
- 对最终损失的影响程度是多少(这叫“梯度”)
反向传播会依赖于“前向传播中产生的中间值”,然后基于链式法则(从输出层一步步往输入层传播梯度,计算损失函数对每一个参数的偏导数)一步步算出这些梯度,接着:
- 每一层根据自己的表现,生成一份“改进建议”——这就是损失函数对每个参数的偏导数,叫作“梯度”
- 每一层保存好这份建议,每层都明确知道该怎么调整
- 最后,这些建议会交给统一的“教官”(优化器)来审核并执行修改,优化器根据梯度和学习率,决定实际的参数更新量
数据流逻辑位置
你可以这样理解整个训练回路:
前向传播:输入图像 → 卷积/池化/全连接 → 输出结果 → 损失函数打分
反向传播:评分结果 → 一层一层往回传 → 每一层知道自己错多少
它就像一份“判决书”,一路传回最前线,告诉基层侦察员:“你上次这句太武断了,下次说话保守点。”
注意,BP(Backpropagation)算法指的是反向传播误差并计算梯度的过程,它本身不包括前向传播,但在实际训练中,前向传播是必不可少的前置步骤,PyTorch 或 TensorFlow 在内部会自动记录前向传播的中间变量,再执行 backward()。所以有些教材或者博客偷懒说:BP算法 = 正向传播 + 反向传播,并不严谨
梯度下降与优化器(Gradient Descent & Optimizers)
当“评分官”(损失函数)给出判断失误的分数,复盘小组(反向传播)已经告诉每一层“哪错了、错得多严重”之后——接下来就需要真正行动起来,调整策略了
这个任务,就交给了训练系统中的教官——也就是优化器(Optimizer)
梯度下降是怎么工作的?
优化器的核心原则叫做梯度下降(Gradient Descent),它是一种古老但高效的参数更新策略
你可以把模型的“判断误差”(损失)想象成一座大山的高度,模型当前所处的“判断方式”就是在山上的某个位置,而它的目标是一步步走到山脚(误差最低点)
梯度就像是“你脚下的坡度”告诉你哪里最陡
梯度下降就是沿着最陡坡往下走一点点,逐步逼近山谷
形象比喻:盲人下山
想象你蒙住眼睛站在山坡上,无法看清远方的地形,但你能感受到脚下哪边更陡
- 你每次迈一步,都朝着坡度最大的方向;
- 你走得越稳,离山底就越近;
- 每次走错方向,评分官(损失)就罚你分数;走对方向,损失值下降,表示你在变聪明
如果学习率太小,就像蜗牛下山,一次迈得很小,走 1 万步才能到谷底,效率极低
如果学习率太大,就像盲人迈大步,可能直接越过最低点反而继续往上冲,甚至来回震荡反弹,永远到不了真正的最优解
所以学习率的设置非常重要:太小学得慢,也容易陷入局部最优解(以为是谷底,其实是小坑,炒股票的懂得都懂),太大学不到(无法抄底)
优化器登场:不同风格的“训练教官”
在实际深度学习中,直接使用基本梯度下降并不稳定,于是人们提出了许多更聪明的优化算法,它们相当于拥有不同风格的教官:
| 优化器 | 特点和比喻 |
|---|
| SGD(随机梯度下降) | 每次只用部分样本来更新,训练更快;带点“试错风格”的老师 |
| Momentum(动量法) | 带“惯性”,像走路带点冲劲,能跳出小坑不反复横跳 |
| AdaGrad / RMSProp | 会“因材施教”,给不同参数安排不同学习速度 |
| Adam | 集大成者,兼具惯性和自适应调整,是目前最常用的优化器之一 |
这些优化器虽然各有不同,但目标一致:让模型更快、更稳地走向误差最小的方向
到这里,我们已经走完了 CNN 从输入图像、提取特征、生成判断、复盘改进、训练收敛的完整流程
接下来,我们 逐层拆解 LeNet ,CNN 的“经典入门模型”——LeNet-5,它是由 Yann LeCun 在 1998 年提出的结构,曾用于手写数字识别,是深度学习发展初期的奠基之作









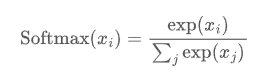



Comments | NOTHING